In real life people have and use a variety of list-like abstractions: shopping lists, bucket lists, and to-do lists, to name a few. These abstractions and the way they are used have two things in common:

• the list contains items of similar character (i.e., the shopping list contains things that can be found in a store, the to-do list has tasks that need to be done), and
• there are actions taken for each item on the list (i.e., find and purchase an item on the shopping list, do a task on the to-do list).

The shopping list is an abstraction because the items on the list are the names of the real-world things to be purchased, not the actual things themselves.

In a similar way, computers have and use real-world abstractions by combining:

• lists - data values of the same type (e.g., type int) representing a real-world abstraction, and
• list iteration - the algorithmic device to process the elements of the list.

The term  "list iteration" means performing the same processing steps on each element of the list, one element at a time. 

An important fact is that the same list iteration can process a list with only a few value or a list with millions of values! The ability of list iteration to process a list of any size gives computing its "power". Many machines generate physical power by performing a mechanical action repetitively: the repetitive motion of the pistons in an internal combustion engine generates the physical power needed to move a vehicle. By analogy, the repetitive processing of list items by an algorithm using list iteration generates the information processing power needed to analyze abstractions having many - perhaps a very large number - of instances. Imagine computing the average household income from the U.S. Census data. The abstraction of a household is a list of household's incomes, but there are tens of millions of instances of this abstraction. List iteration is critical in this case because it allows the same steps to be repeated for each instance. Using list iteration simple quantitative measures, like an average, can be computed for the values in the list.

List Iteration: An Interactive Introduction

Interactive animations will be used to explore the dynamic process of list iteration in three steps:

Step 1: an "iteration variable" holds each successive value of the list; a set of actions are performed with each new value

Step 2: the value of the iteration variable can be used by the actions performed on each new value

Step 3: the iteration variable and other variables in the program's state can be used in the actions to compute a quantitative measure of the list.

Generally, in the animations:

• a list is drawn as a green horizontal set of adjacent boxes,
• actions are drawn as blue rounded rectangles ,
• the list iteration is a complex shape with
  • the words "for each item" above a window through which a value in the list is visible, and
  • an open notch with the label "do" to hold the actions taken on each step of the list iteration.

Each animation has controls to move the animation forward (>), backward (<), to the beginning (<<), or to the end (>>). A pair of numbers in the upper left-hand corner shows which slide is currently being viewed and how many slides there are in the animation.

Step 1: an "iteration variable" holds each successive value of the list; a set of actions are performed with each new value.

 

 

Step 2: the value of the iteration variable can be used by the actions performed on each new value.

 

Step 3: the iteration variable and other variables in the program's state can be used in the actions to compute a quantitative measure of the list.

Computing a quantitative measure requires two ideas:

• accumulation, and
• initialization.

Accumulation means that an algorithm collects information on each cycle of the iteration that is remembered from one cycle to the next. For example, consider how to find the sum of all the values in a list. How is it possible to find the sum if the iteration variable only gives one value in the list? The answer is that the algorithm needs an additional "accumulation" variable whose value is the sum of all the values seen prior to the "current" element. On each cycle of the iteration, the accumulation variable is updated by including in its value the value of the iteration variable. 

Initialization means that the accumulation variable must be given an initial value before the iteration begins. Initialization is necessary so that accumulation variable has a "starting point" for the updating that is done on each cycle of the iteration.

The ideas of accumulation and initialization are illustrated in the following interactive animation that computes a simple quantitative measure (the sum of the value in a list).

Lists in BlockPy

An example of a list in BlockPy is shown in the following figure. The arrows in this figure show how the blocks would be assembled to form a list of three numbers that is set as the value for a property. The create list with block is found in the Lists menu. The numbers are in the Values menu and the set block is in the Variable menu.

Creating a List

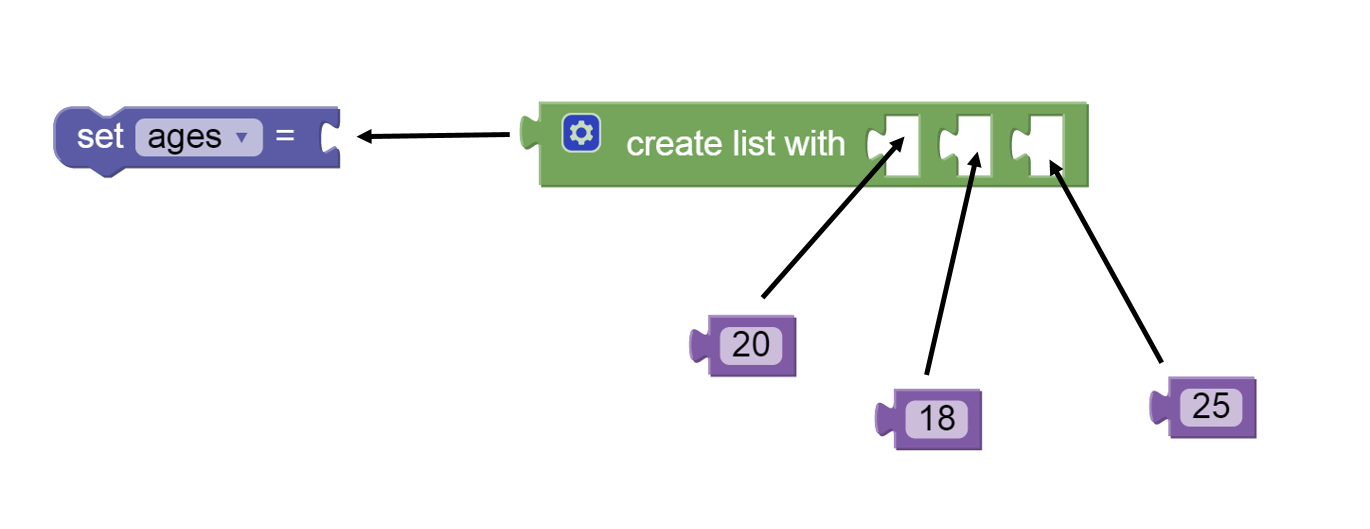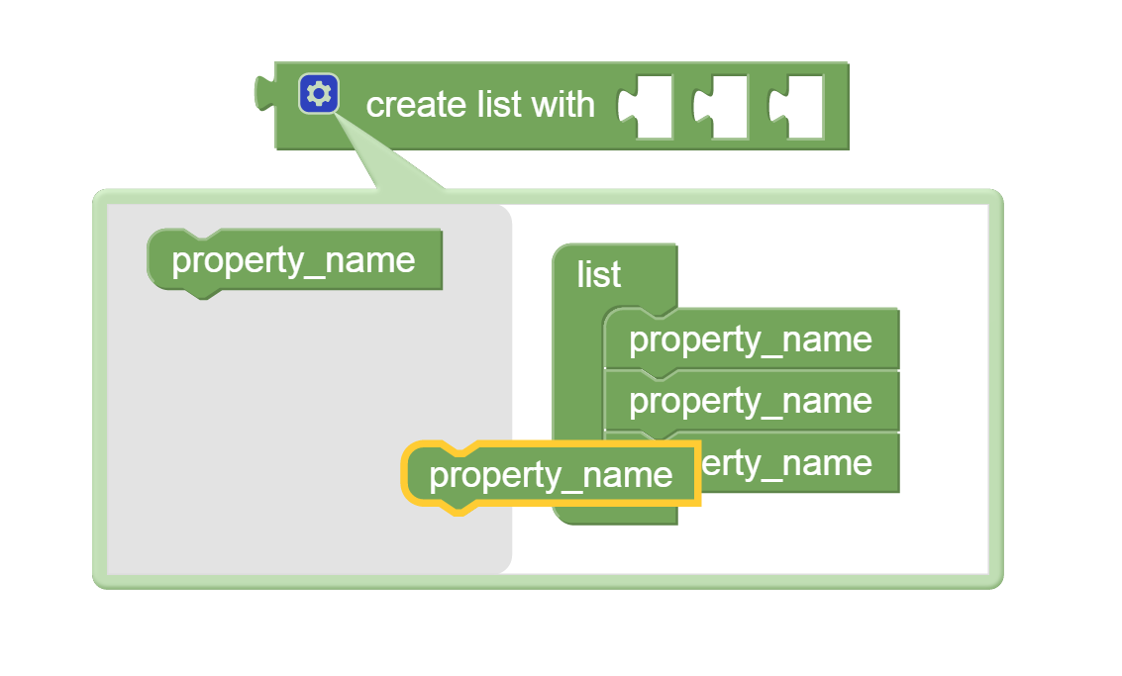
 By default the create list with block creates a list with slots for three elements. Of course, a list with more or fewer slots for elements may be needed. For this reason the create list with block can be edited to add or remove slots.The figure below shows an example of the editing

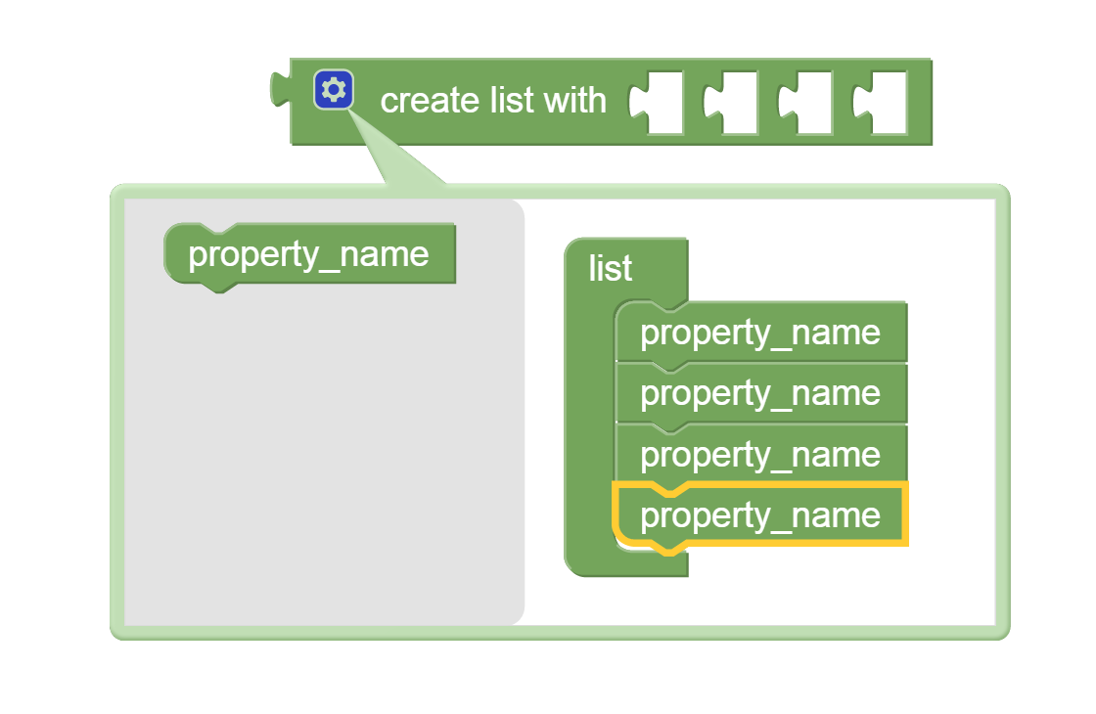Editing the create list with block

To begin adding new list elements click on the blue colored gear symbol in front of the word "create" on the create list with block. This pops up the editing menu shown in the left part of the figure above. The block labelled property_name can be dragged from the gray area to the list grouping. The left part of the above figure shows a highlighted property_name block in the act of being dragged in this way. When the property_name block is inserted into the list group a new slot is added to the create list with block. As many slots as needed can be added in this way by repeatedly dragging a property_name block from the gray area to the list group. When done adding new list elements, click on the blue colored gear symbol to collapse the editing menu. 

To remove list elements begin by clicking on the blue colored gear icon. In the editing menu move a property_name block from the list group to the gray area to its left. This will shorten the list group and remove the corresponding slot from the create list with block. 

List Iteration in BlockPy

Example 1.

Below is a live BlockPy workspace that illustrates a list and list iteration. This program prints each element of a list that has five values. This program expresses in BlockPy the same iteration as the second interactive animation above. The iteration block is in the Iteration menu and the print block is in the Output menu.

Run this program (using the Run button) and observe the output displayed in the Printer box (immediately above the BlockPy canvas). 

Experiment with the above workspace to

• add and remove values from the list,
• change the values in the list, 

The Reset button can be used to restore the workspace to its original condition. Resolve any questions or issues that you encounter in working with this simple list.

Example 2.

Below is a second BlockPy work space that a program to compute the sum of the elements in a list. This program expresses in BlockPy the same iteration as the third interactive animation above. The blocks to perform addition (and other mathematical operations) are in the Calculation menu.

Run the example algorithm and observe the output that it generates in the Printer area at the top of the workspace.

This algorithm proceeds through five iteration cycles as shown in the following table. Notice that on each iteration the value of the iteration variable changes. On each iteration the iteration variable has the same value as an item on the list.

The critical importance of iteration is that it works for lists of any length. Using the above work space add several more elements to the list and observe that the iteration without change works for this longer list.